Have you ever been in a team planning session and heard “I’ve found the most incredible strategy for teaching my students multi-digit multiplication”? However, how do you evaluate the usefulness and appropriateness of non-traditional multiplication methods? Today, I share two considerations to determine whether an alternative strategy is appropriate to use with students.
“Hey, Beth! I found the coolest strategy to teach my students how to multiply two-digit numbers.”
“Oh, really! What strategy is that?” Beth said.
Beth listened intently while I explained the new strategy I discovered when preparing for my unit on two-digit multiplication.
When I finished, Beth said, “Shametria, how will that help students multiply decimals?”
I didn’t have an answer.
In my excitement, I had not considered the long-term implications of teaching my students this method rather than one that would support students later.
Lesson Learned
Beth and I had been friends since college. We both selected the math specialization certification path in college, so we often shared our experiences with each other once we started teaching. Beth taught middle school and I taught fourth grade, so I was excited to share my discovery with her but was disappointed when my excitement met with silence and a scolding.
The Problem with Non-Traditional Multiplication Methods
I was so thrilled about using this strategy with my students who had been unsuccessful with the standard algorithm that I forgot to consider how the strategy would help my students in the future.
There are many non-traditional multiplication methods floating around in textbooks and on the web to help us teach two-digit multiplication. However, it’s important we ask ourselves the following questions when selecting an alternative strategy to use.
- Is the strategy mathematical?
- Will the strategy support the learning of operations later in a student’s mathematical career?
Let’s use the lattice method to consider the questions above.
Explore the example of the lattice model below. This model shows the solution for 87 x 24. The lattice strategy requires students to multiply each digit on the top by each digit on the right side, place their product into the intersecting box in the array, and add the diagonal “lines” to get the product.
![[Insert Lattice Method here; Alt text: This is an example of one of the non-traditional multiplication methods.]](https://www.therouttymathteacher.com/wp-content/uploads/2021/09/Lattice-Method-min-1024x896.png)
Is this multiplication strategy mathematical?
The Common Core State Standards for Math emphasize a progression of computational strategies be used to help students build an understanding of the more-standard algorithm (Fuson and Beckmann, 2012). This means non-traditional multiplication methods should emphasize place value concepts as related to the computation process and the properties of operations.
If the lattice model reinforced these important mathematical understandings, students would leave with the understanding that when the model shows 7 x 2 = 14, the meaning is actually 7 x 20 = 140. Now, I know what you’re thinking– the standard algorithm presents the same limitation; however, the formatting of the lattice method makes it more challenging for students to easily see the place value of each number.
Will the multiplication strategy support the learning of operations later in a student’s mathematical career?
My middle school math friend argued this method does not work well with decimals and therefore, in her opinion, would not support students as learning progresses into the middle grades. However, much like the traditional algorithm, students can total the number of digits on the right side of the decimal in both factors and then count that number of places from the last digit in the product to know where to place the decimal.
So what now?
Formatting is the major issue here. The lattice method does not communicate place value well. A solid understanding of place value is essential to the conceptual development and understanding of decimal multiplication. In fact, if you modify the lattice model to emphasize place value, you get another model– the area model (see the image below).
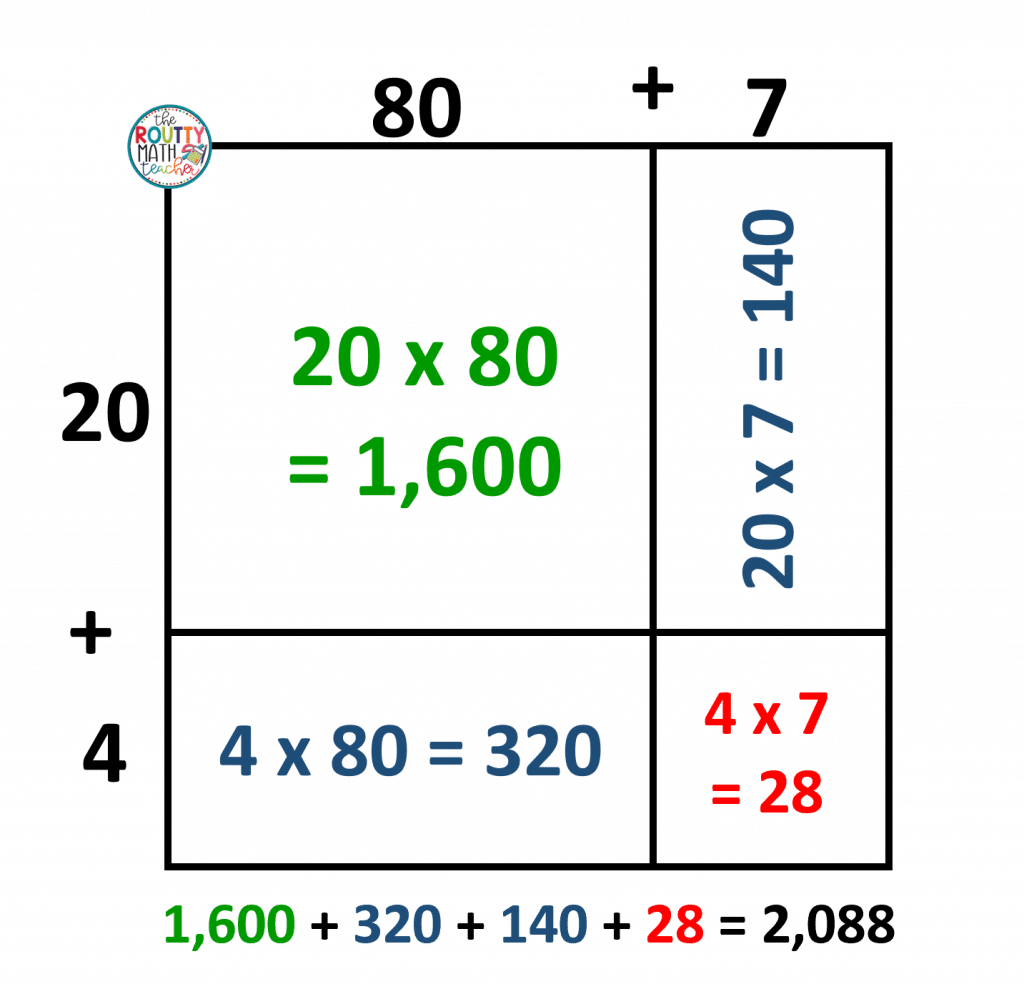
The area model accomplishes the same goal as the lattice method and is visually similar. It will also help students multiply with decimals effectively once students have developed the concept of decimal multiplication.
The area model also lends itself to a strategy Algebra teachers use to teach the multiplication of polynomials. For example, students can use a similar model to multiply (x + 2) by (x – 3).
As teachers, we are always on the lookout for ways to better help our students master the curriculum. However, it’s important to make certain the strategies we choose will support them beyond their time in our classrooms.
Sound Off!
What are your favorite non-traditional multiplication strategies? Respond in the comments below.
Reference:
Fuson, K. C., Beckmann, S. (2012). Standard algorithms in the common core state standards. NCSM Journal, pp. 14-30.