Teaching students to multiply larger numbers is a real challenge for many teachers; however, developing a solid understanding of this process is the foundation for learning more algorithmic procedures later. Starting with a manipulative, like Base 10 blocks, helps students build a conceptual understanding that will help them understand the algorithm later. In today’s post, I share ways to use Base 10 blocks to develop two-digit multiplication skills.
The hardest part of my first year teaching was teaching math.
I honestly can’t believe I just said that, but it was!
I realized things that were easy for me to do were not easy to teach.
For example, I can calculate elapsed time in my head with minimal effort, but teaching it to fourth graders– wow, just wow.
Teaching two-digit multiplication was also an experience I will never forget.
I was on alternative strategy number four before I could see the light at the end of the tunnel.
It was painful and we spent weeks slugging through practice problem after practice problem.
Two-digit multiplication was easy for me, so why couldn’t I teach my students?
Building Fluency with Two-Digit Multiplication
This challenge brought many restless nights and even a little desperation. Why was this so hard?
Some years ago, I started using Base 10 blocks to introduce multiplication with larger numbers. Using Base 10 blocks in this way was new for me because it’s not the way I learned; however, my students found a great deal of success with this tool and it provided a more solid foundation for using the algorithm to multiply with larger numbers later.
Why Not the Standard Algorithm?
We’ve all been there. Your two-digit multiplication unit rolls around and you feel pressured, either by your colleagues or well-intentioned homework-helping parents, to just teach the standard algorithm. After all, why does it matter?
The National Council of Teachers of Mathematics state the “effective teaching of mathematics builds fluency with procedures on a foundation of conceptual understanding so that students, over time, become skillful in using procedures flexibly as they solve contextual and mathematical problems” (Principles to Actions: Ensuring Mathematical Success for All, p. 42).
What is Fluency?
Fluency is a student’s ability to “choose flexibly among methods and strategies to solve contextual and mathematical problems” (p. 42).
Selecting strategies “strongly related to number sense” forces students to go beyond memorizing basic facts or a series of steps not connected to meaning (p. 42).
Trying to rush students to develop fluency before they are ready can even cause some of our students to develop math anxiety. (Read Jo Boaler’s Fluency Without Fear article!)
How to Build Procedural Fluency of Two-Digit Multiplication from Conceptual Understanding
Using Base 10 blocks to model two-digit multiplication is a great way to use a model and connect to the algorithm at the same time.
In the picture below, I model how Base 10 blocks can be used side-by-side with a multiplication area model to illustrate the connection between an area model for multiplication and its often confusing and hard-to-understand algorithm.
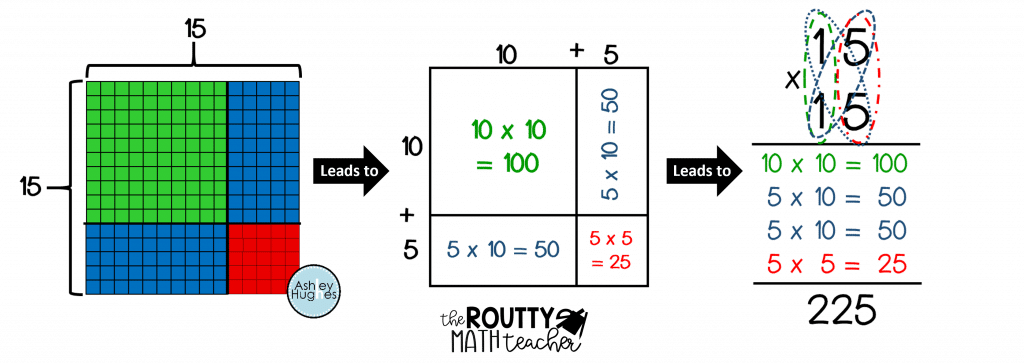
Specifically, the model shows how using Base 10 blocks to model two-digit by two-digit multiplication relates to the area model and the traditional algorithm. Here’s how it works:
- First, students break down two-digit numbers into tens and ones and create a rectangle using the two factors as the side lengths. This provides students with a visual of the product.
- Second, students begin drawing a model of the Base 10 blocks and label the side lengths and inside areas. Then, they add all four areas to find the total.
- Third, students connect the area model to the partial products strategy using a familiar format.
- Finally, students use the traditional algorithm with a correct understanding of place value.
Starting on the Right Foot
When students first begin two-digit multiplication, we often jump to using the algorithm too quickly. Students need time to develop multi-digit computation skills to build a solid foundation for the algorithms later.
Consider how using the strategies above may help your students develop fluency in multiplying multi-digit numbers. In fact, both the Texas standards and the Common Core standards emphasize the use of strategies to develop multiplication skills.
Sound Off!
How do you help students understand the traditional algorithm? Respond in the comments below.
References:
- Boaler, Jo. (2015, January 28). Fluency without fear. https://www.youcubed.org/evidence/fluency-without-fear/
- National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematical success for all, p. 42-48.





