
Today’s post is inspired by a conversation I had recently with a teacher with whom I work. I was meeting with her to discuss a state assessment that we are required to give to our English Language Learners but we ended up discussing a mathematical writing task she had given her students. As I reflected on the conversation later, it really reminded me of the importance of understanding what our students understand about math and the importance of developing a conceptual understanding before developing a procedural understanding.
The writing task that was given to her students was a culminating formative assessment of fraction operations, a huge topic for fifth graders across the U.S. The task is illustrated in the image below. Students were asked to complete the task without doing any computations but with just a justification for their answer.
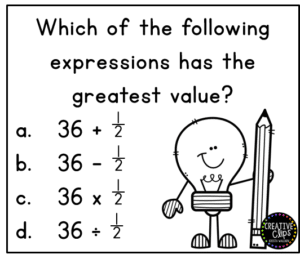
As we discussed the task further and I read some of the students’ responses, I was shocked to learn that some students had an incomplete understanding of fraction operations altogether, such as selecting the multiplication expression because multiplication always yields a larger quantity. While this is a difficult topic for some students to grasp, it is an essential understanding of rational number operations.
The most widely given response was the correct response– the division expression. I was initially very excited about the students’ responses, but I quickly realized that they left a lot more to be desired. The response below represents the most common response.

Many people who read this post, may think, “What’s wrong with this response?” The truth is that this student is certainly able to select the right response and use a common algorithm correctly, but s/he does not have an understanding of fraction operations. Understanding fraction operations means making sense of the seemingly contradictory situation where multiplying yields less and dividing yields more. Students who have a conceptual understanding are able to blend this knowledge with their understanding of whole numbers for a complete understanding of how operators change outcomes when computations involve values that are less than one, greater than one, or a mix of both.
The Common Core Standards State Initiative website (www.corestandards.org) defines rigor as a “deep, authentic command of mathematical concepts.” The authors urge “to help students meet the standards, educators will need to pursue, with equal intensity, three aspects of rigor in the major work of each grade: conceptual understanding, procedural skills and fluency, and application” (From Other Resources > Key Shifts in Mathematics). In addition, The National Council of Teachers of Mathematics states that the “effective teaching of mathematics builds fluency with procedures on a foundation of conceptual understanding” (Principles to Actions, p. 42).
If I use this principle as a method for evaluating the student response above, I can see that the student has developed some procedural fluency, but it appears that the student does not have a conceptual understanding of the topic. It’s curious that the students were asked to complete the task without doing any computations, but that is exactly what this student did to find a solution. This deepens my concern even more because it appears that a conceptual understanding may not have been a component of this unit of study.
A student that has a more conceptual understanding of fractions may have provided a response more like the one below. While the response could certainly have included a pictorial model to support the case, this shows a much more solid understanding than the response above illustrates. It’s important to note that both student responses lead to the same algorithm, which is the ultimate goal, but the student response shown below is built from a conceptual understanding of what it means to divide with fractions, a challenging understanding that many adults struggle to attain.

At this time, our conversation takes a different turn as we begin to discuss how to respond to the students whose responses reflected the thinking in the initial response above. personally, I think interviewing students to better understand their thinking is a great next step. I might even ask, “Can you prove your answer is correct in another way?” I may also consider asking if students are able to model their response with a picture. This allows me to circle back to the conceptual piece. If a student has real trouble, I might also ask him/her to put it into context and think about a time when 36 may need to be divided into halves. (Want to know more about how to use and respond to formative assessments? Explore this collection of blog posts!)
So what about the second response? This student has demonstrated both a procedural understanding and a conceptual understanding. As next steps for this student, I may give the student number tiles numbered 0-5 and ask the student to create an expression with a whole number and a fraction that will yield the largest possible value. This task then becomes an application challenge. Can the student take their understanding and apply it? The goal then would become using the largest possible whole number and the smallest possible fraction. (Think: Forty-three divided by one-fifth has a value of 215!) There’s lots of thinking in play here, but students have a real opportunity to demonstrate understanding, especially if students have to justify their thinking.
This scenario gets at the heart of depth of knowledge. In order to have a complete understanding of a topic, students must be able to use their conceptual understanding to develop the procedural understanding and then apply both to application problems. This scenario reminds me of the importance of having students justify their thinking, either orally or in a written format. Imagine if this question were on an assessment. Most of the students would respond correctly, but their responses would be based on an incomplete understanding. It’s only when we dig a little deeper that we uncover the shallowness of students’ understanding and can then develop an appropriate way to respond.
Freebie Alert! Looking for more ways to help students develop a deeper understanding of fraction operations? Check out this freebie pack in my Teachers Pay Teachers Store. Click here or on the image below to grab your copy!
Sound Off! How would you respond to this student misunderstanding? Respond in the comments below.









