Assessing our students doesn’t always need to involve a traditional paper-and-pencil test or quiz. In this post, I share five formative math assessment examples to help you drive instruction.
As a student, when I heard the word assessment, I knew it meant a quiz or a test was on the horizon.
And, it usually meant it was a BIG deal!
So, it’s no surprise I carried this line of thinking with me into the classroom.
If I wanted to assess my students’ understanding, I needed to create a quiz or a test, right?
It wasn’t until I started working on the culminating research paper for my Master’s degree that I discovered there were more ways for me to assess my students than with a paper-and-pencil task.
In fact, my journey into alternative math assessments led me to my love of math journals.
It also opened my eyes to the world of formative assessments.
Since then, I’ve never looked at math the same way. I’ve made a career out of finding new ways to better understand what our students know and understand about math.
There’s a Better Way
Using a variety of ongoing assessment techniques is an important way to assess how students are progressing toward mastery.
Traditional methods include tests and quizzes; however, there are a host of other tools that will not only keep your students engaged but will also provide the feedback you need to get a gauge on your students’ understanding.
Using student feedback and data to drive our instructional decisions cuts down on the time spent teaching concepts and skills our students already know or aren’t ready for yet.
Formative Math Assessment Examples
One of the best ways I found to assess student learning is through writing. There’s something about reading a student’s reasoning that allows me a glimpse into their thinking. It also helps me know where to go next in instruction.
With this in mind, I want to share five of my favorite formative math assessment examples which assess student understanding through writing. Each of the strategies is a formative tool designed to provide feedback on student understanding of a lesson objective or learning target.
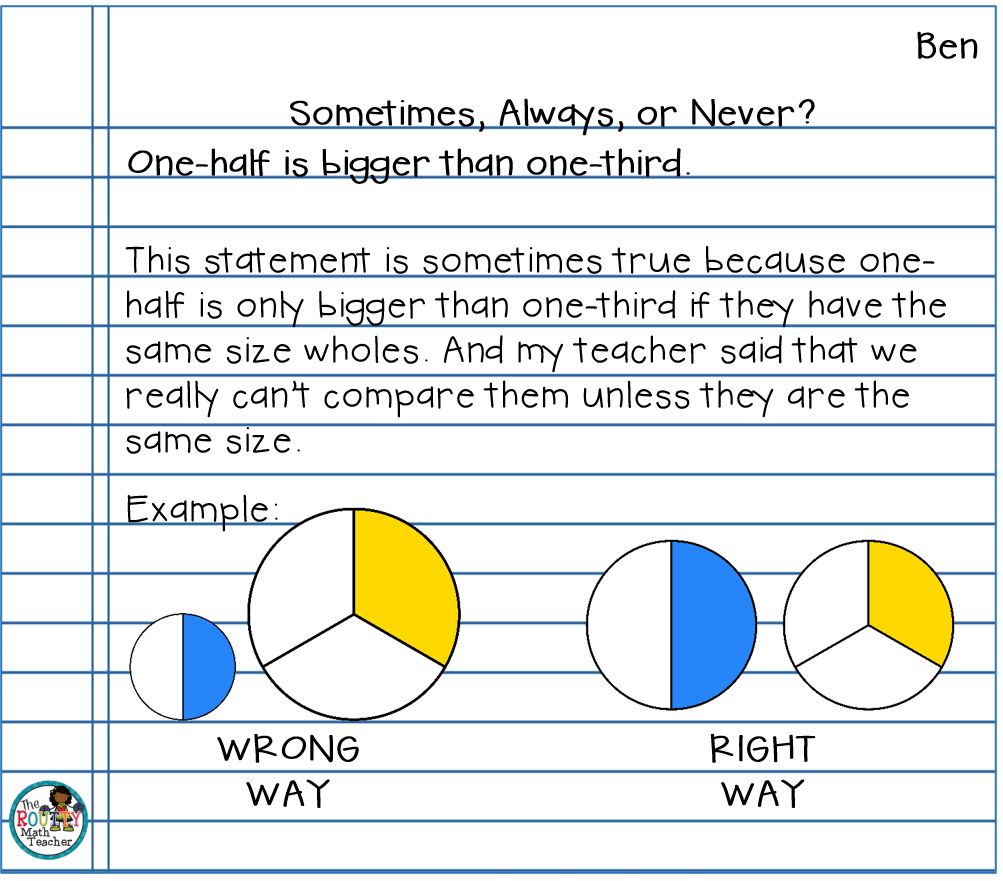
Sometimes, Always, or Never*
For this strategy, students are given a statement and must determine whether the statement is always true, sometimes true, or never true. To do this, students must consider all of their options by selecting instances of and trying to create a generalization for the concept.
Here’s how it works:
- Post the lesson objectives in specific, kid-friendly language.
- Give each student a small slip of paper or an index card.
- Create a statement, based on the lesson objections, to which students can respond with “sometimes,” “always,” or “never.” Note: Responding in writing will boost all the students’ critical thinking skills, but creating a statement with a “sometimes” response gives you a more comprehensive picture of your students’ progress toward understanding the learning objective.
- Ask students to respond to the statement with “sometimes true,” “always true,” or “never true” and give a justification in pictures, words, or numbers.

Fact or Fib*
For this strategy, students determine whether a statement is a fact or a fib. Like the Sometimes, Always or Never strategy, the power comes from the justification piece. It is not enough for students to respond with fact or fib, they must know why and be able to communicate their thinking in pictures, words, or numbers.
Here’s how it works:
- Post the lesson objectives in specific, kid-friendly language.
- Give each student a small slip of paper or an index card.
- Create a statement, based on the lesson objectives, to which students can respond “fact” or “fib.”
- Ask students to respond to the statement with “fact” or “fib” and give a justification in pictures, words, or numbers.
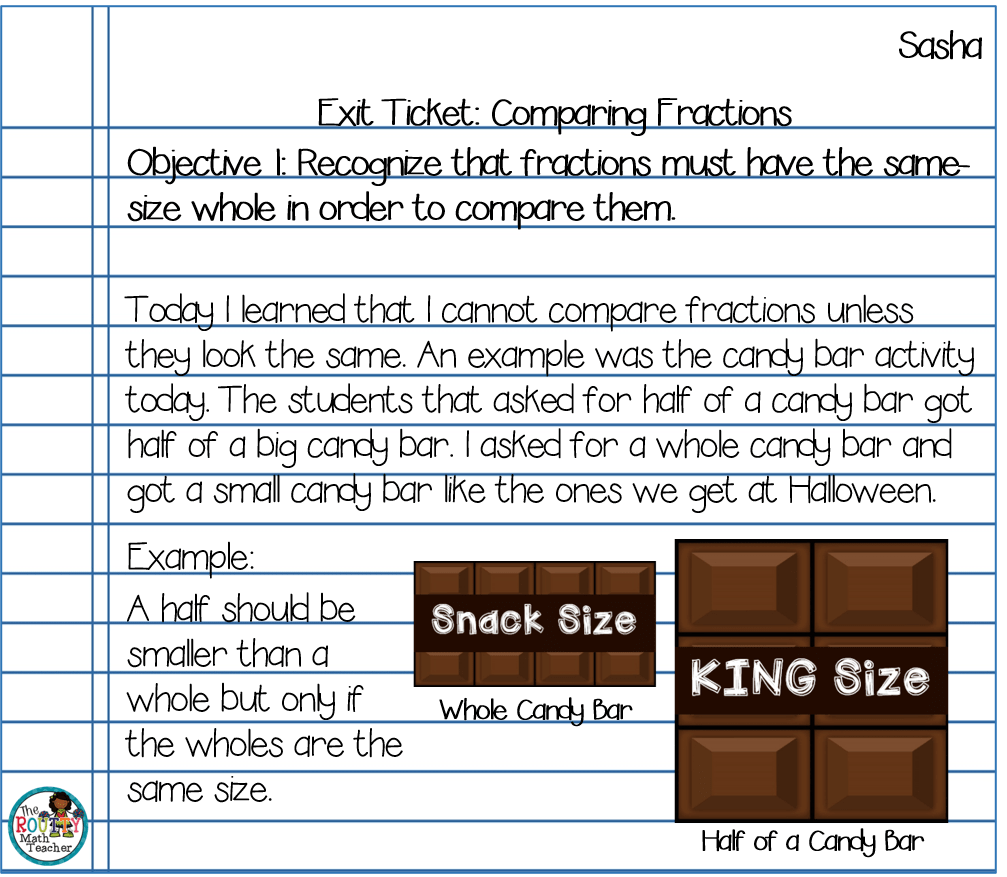
Exit Tickets with Understanding*
You may be familiar with traditional exit tickets where students complete a problem or write about a skill or concept on a small slip of paper at the end of class. The kicked-up version of this uses the same concept except students write about their understanding of the lesson objectives. This allows the teacher an opportunity to get a glimpse of where each student is in their thinking about and development of the objectives of a targeted concept or skill.
Here’s how it works:
- Post the lesson objectives in specific, kid-friendly language.
- Give each student a small slip of paper.
- Students choose an objective, or one suggested by you, and provide evidence of their understanding. For example, ask students to share their thoughts in pictures, words, or numbers.
- Collect the students’ responses. Sort the student responses based on levels of student understanding. Use the feedback to determine the next steps in instruction.
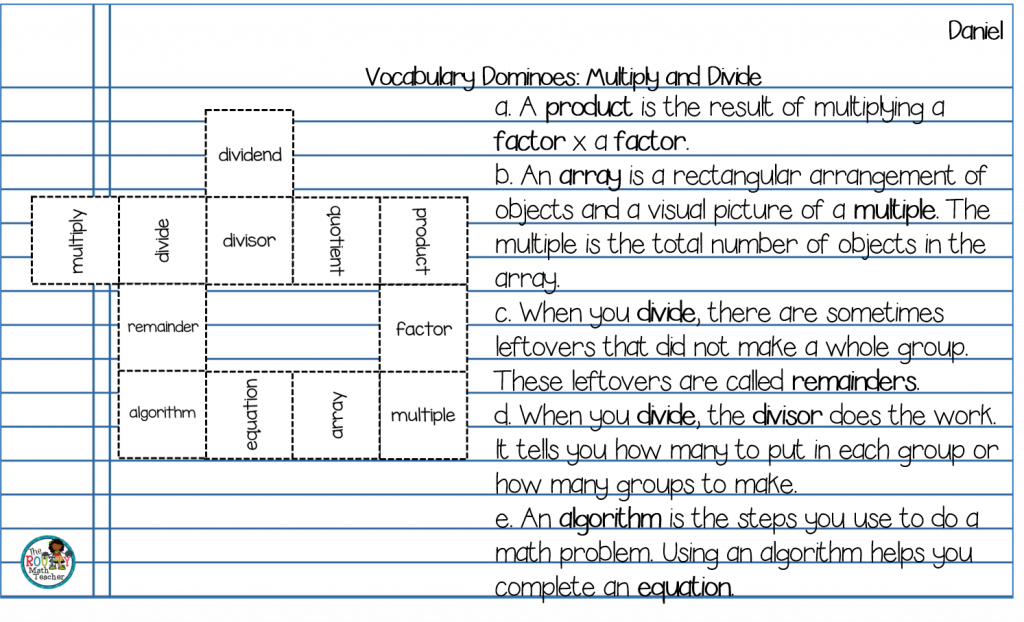
Vocabulary Dominoes*
This activity requires students to compare and contrast terms, as well as, look for, analyze, justify, and communicate about relationships as they connect “dominoes” to illustrate connections.
Here’s how it works:
- Program a set of vocabulary dominoes with content-specific math terms. Note: I intentionally placed words whose relationships were easily identifiable on the same domino so that students have to explore other relationships.
- Decide in advance whether you want students to create their own arrangement or if you will create one for them to use. Note: There are advantages to both approaches. The first approach allows you to gain knowledge regarding an individual student’s understanding of the terms; whereas the second method forces the students to make judgments and find relationships based on someone else’s thinking. In addition, the second method may take less time because students will not need time to create their layout.
- If students are creating their own arrangement, provide them time to cut-out and arrange their dominoes based on the relationships between the words. If you are using a teacher-created arrangement, provide students think-time to review the layout and placement of the words.
- Ask students to write 3 – 4 statements regarding the relationship of the terms based on the connections made.

Who’s Correct?
This assessment tool allows students the opportunity to evaluate the mathematical thinking of others and either agree or disagree with the person’s response.
Here’s how it works:
- Present a problem to the class along with four characters’ answers and reasoning.
- Individually, have students determine who is correct and explain why.
- After students have selected the response(s) they believe to be correct, have them provide a justification for why the other responses are incorrect.
Driving Instruction
Creating engaging opportunities using the formative math assessment examples above provides teachers with rich information about student understanding of a selected content standard.
This information can then be used to make more informed decisions to move students forward or provide necessary interventions.
Ready to get started? Download my Let’s Write ebook which includes formative math assessment examples and ready-to-use templates using the form below.
Sound Off!
Which strategy do you think would provide you with the most useful student information? Respond in the comments section.
References:
* Adapted from Lead4ward
Credits:
Clipart courtesy of Zip-A-Dee-Doo-Dah Designs, Fun for Learning, and Creative Clips.






2 Responses
Dear Shametria,
I am a huge fan of your strategy #5 Who’s Correct? This is a great activity that allows students to meet common core practice standard number 3 where students are able to construct viable arguments and critique the reasoning of others. Presenting this question is a great low floor, high ceiling task. All students can contribute to the conversation about who they agree or disagree with, and then students are able to take it to a higher level of thinking by correcting the mistakes or supporting their arguments. What are some ways to have students converse using mathematical language during this activity and have them take lead of the conversation with their thoughts ?
Thank you,
Pre-service Teacher Vishna
Hello! I agree with you! This is a great way to help students practice critiquing the thinking of others. In terms of having students participate in math talk, each response can be assigned a corner of the room and students can go to the corner of the solution they chose and discuss why they selected that response. As an alternative, you can assign students to a particular corner and have them debate whether the response is correct or not. If the response is incorrect, students can discuss what went wrong and decide on the best way to help the person correct their thinking or their work.