Place Value Relationships

You want me to teach . . . place value relationships? What on Earth does that mean? 

It was always the first lesson of the year . . . place value — Ugh! 

I went to my math storage area and pulled out sets of Base 10 Blocks, place value mats, and dry erase materials as I prepared for the next day’s lesson. 

I had done the same lesson at least 20 times. We modeled numbers with Base 10 Blocks to help students “see” the number in a hands-on way. Then we moved to reading and writing numbers in number form, word form, and expanded form. 

Fast forward about 10 years. The standards have changed. 

Now, instead of just teaching students how to read and write numbers, we are required to teach students to recognize a digit in the tens place is ten times greater than the same digit that is one place to its right, the ones place. 

That just sounds complicated, right? 

And now I have to teach it to kids . . . oh my word!

So what does this standard really mean– in simple terms? 

According to Gojak and Miles (2016), this standard

• Relates the relationship of the values of the digits in a number to multiplication and division
• Connects to multiplying and dividing by multiples of 10

Relationship Between The Places: Moving To The Left

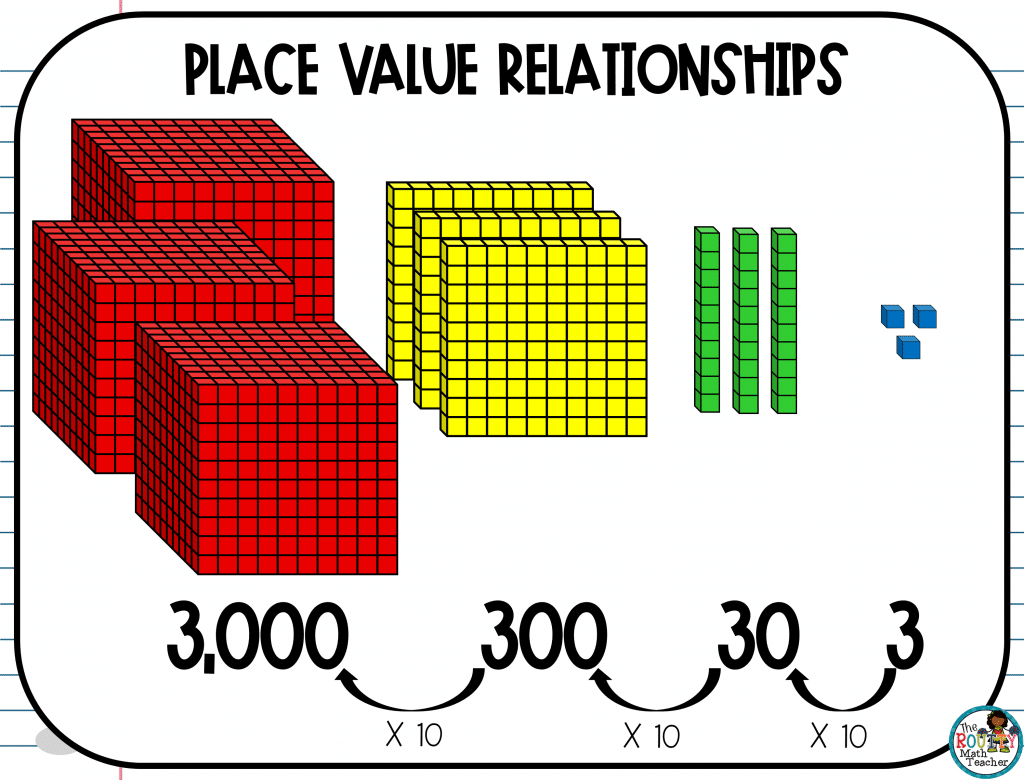
Notice the value of the Base 10 Blocks on the far right have a value of 3. Observe what happens each time we move to the left. 

The value of the blocks is 10 times greater than the previous set of blocks. Thus, the value of the 3 is 10 times greater as well.

• When we move one place to the left from the ones place (3), the tens place (30) is 10 times greater than the ones place. 
• Moving one place to the left from the tens place (30), the hundreds place (300) is 10 times greater than the tens place.
• When we move one place to the left from the hundreds place (300), the thousands place (3,000) is 10 times greater than the hundreds place.  

Relationship Between The Places: Moving To The Right

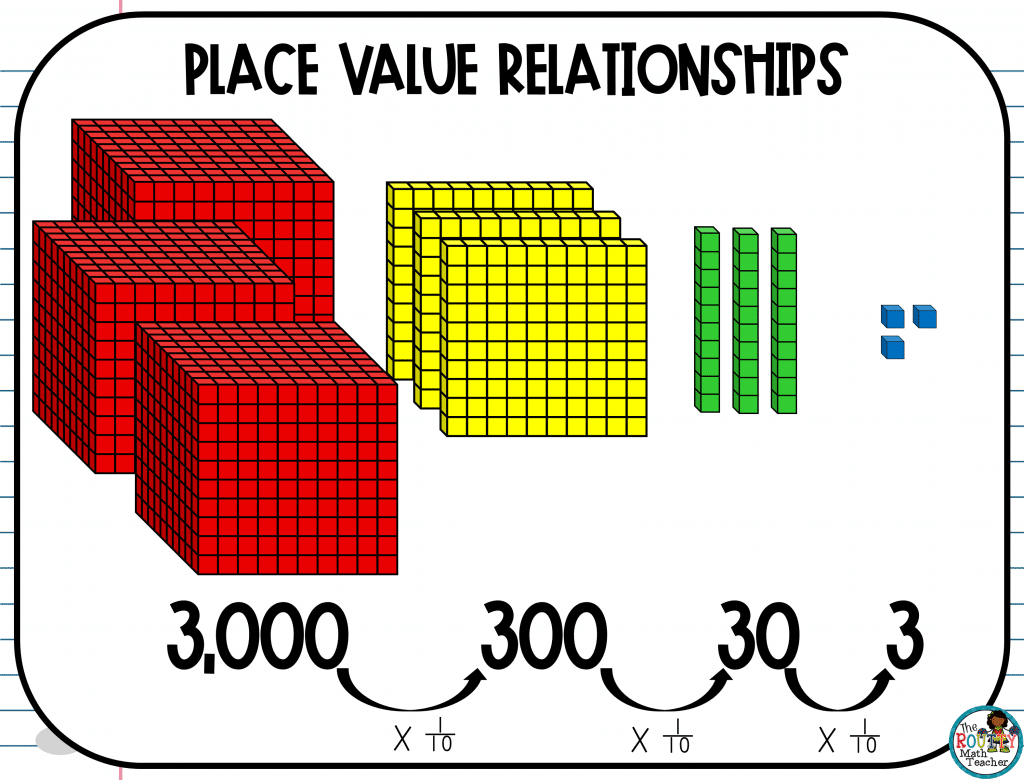
Now, notice the value of the Base 10 Blocks on the far left have a value of 3,000. 

Each time we move to the right, the value of the blocks is one-tenth of the previous set of blocks. Thus, the value of the 3 is one-tenth of the previous value.

• When we move one place to the right from the thousands place (3,000), the hundreds place (300) is one-tenth of the thousands place. Think: 3,000 ÷ 10 = 300.  
• Moving one place to the right from the hundreds place (300), the tens place (30) is one-tenth of the hundreds place. Think: 300 ÷ 10 = 30.  
• When we move one place to the right from the tens place (30), the ones place (3) is one-tenth of the tens place. Think: 30 ÷ 10 = 3.  

How Do Decimals Fit Into The Picture?

Using Base 10 Blocks to represent the relationship between decimal values requires a bit of a shift in thinking. 

The relationships follow the same rules from left to right and right to left; however, more attention is needed to ensure decimal values are represented correctly. 

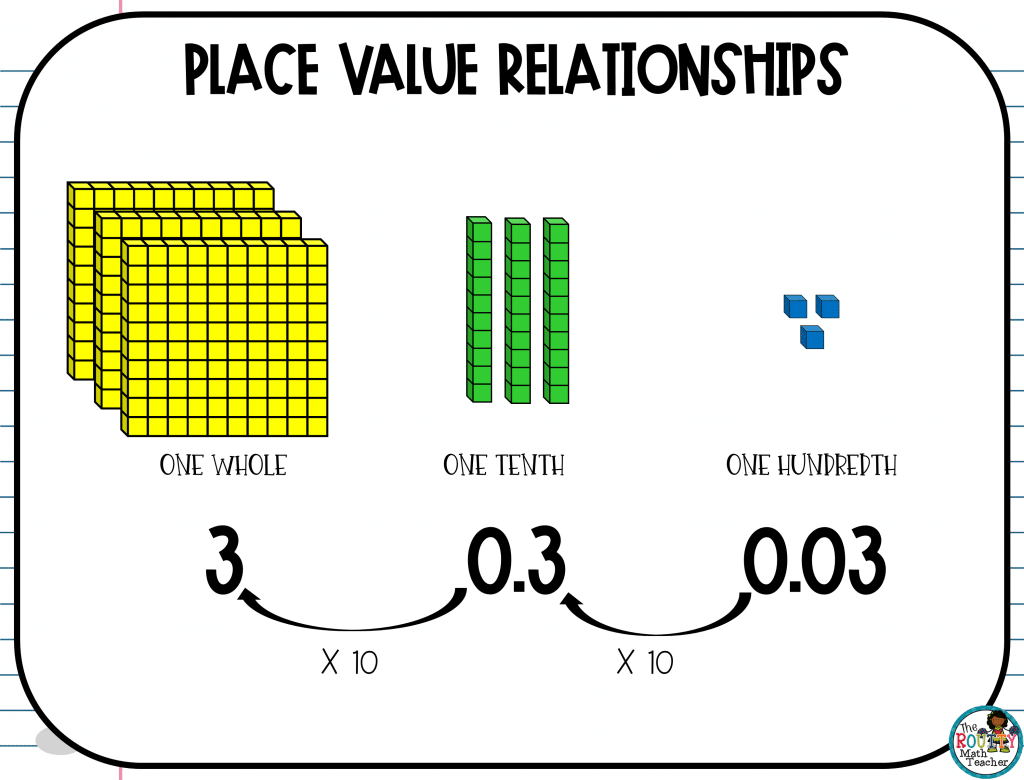
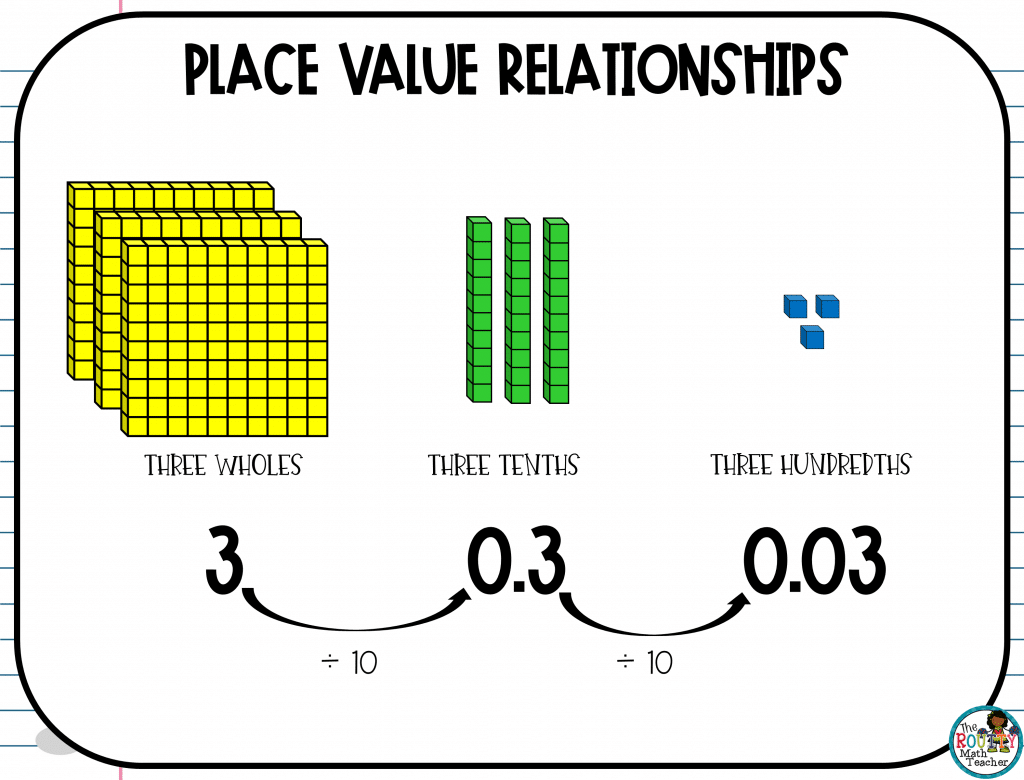
Ways To Help Students Understand Place Value Relationships

Students need many opportunities to explore this concept and explain the relationship between the same digits in different numbers. 

Follow-up activities:

1. Have students compare the value of the same digit in different numbers. For example, ask students, “How does the value of the 7 in 10,749 compare with the 7 in 8,567?” Then have students use mathematical language to explain the comparison.
2. Look at patterns of numbers such as 4, 40, 400, 4,000, and 40,000 and have students extend the pattern and explain what happens to the value of the four as you move from left to right or right to left. 
3. Give students a number and ask them to record a number which includes a specific digit that has a value related to the original number. For example, say, “Write a number where the nine has a value that is 100 times greater than the value of the nine in 911.” Or, say, “Write a number where the two has a value which is one-tenth of the value of the two in 2.56.” Students can then record their responses on a dry erase board and share/justify them to a partner. 

Communicating About Place Value Relationships

Providing a variety of place value activities and games to reinforce this concept is essential to student mastery. Students should also be encouraged to identify the relationship between places in numbers as “_____ times greater” or ______ (fraction) of the value of the [insert digit] in the [insert previous place].” 

Making connections to multiplying by multiples of 10 (moving from right to left) or dividing by multiples of 10 (moving from left to right) can be reinforced at this time as well. 

Final Thoughts

For many students, the abstractness of understanding place value relationships is confusing. Using manipulatives, such as Base 10 Blocks, to model numbers and make visual connections help students understand the skill. 

Recognizing a digit in the tens place is ten times greater than the same digit that is one place to its right, in the ones place, doesn’t have to be complicated. With manipulatives, standards-based activities, and opportunities to explain their thinking, students will be able to articulate the relationship between place values. 

Ready to jump in? Grab my free place value dice game using the form below.  

Sound Off!

What strategies do you use to help your students understand place value relationships?

References

Gojak, L. M. & Miles, R. H. (2016). The Common Core Mathematics Companion: The Standards Decoded. Thousand Oaks, California: Corwin.