
Fractions. A single word that deflates the confidence of our most competent students and adults alike. In fact, I am sure that many readers are reliving their own fraction experiences as they read this post– good or bad! I can’t say that I myself don’t have certain feelings about my own experiences with learning fractions, but over the years, I have developed a deeper understanding of fraction concepts through my experience as a teacher, a mathematics education graduate student and also as a math coach. Today, I want to highlight different fraction tools that can be used to help students make sense of fractions and address specific Common Core State Standards for Math.
Pattern Blocks
Common Core State Standard 3.NF.A.1- Understand a fraction 1/b as the quantity formed by 1 part when a whole is partitioned into b equal parts; understand a quantity a/b as the quantity formed by a parts as size 1/b.
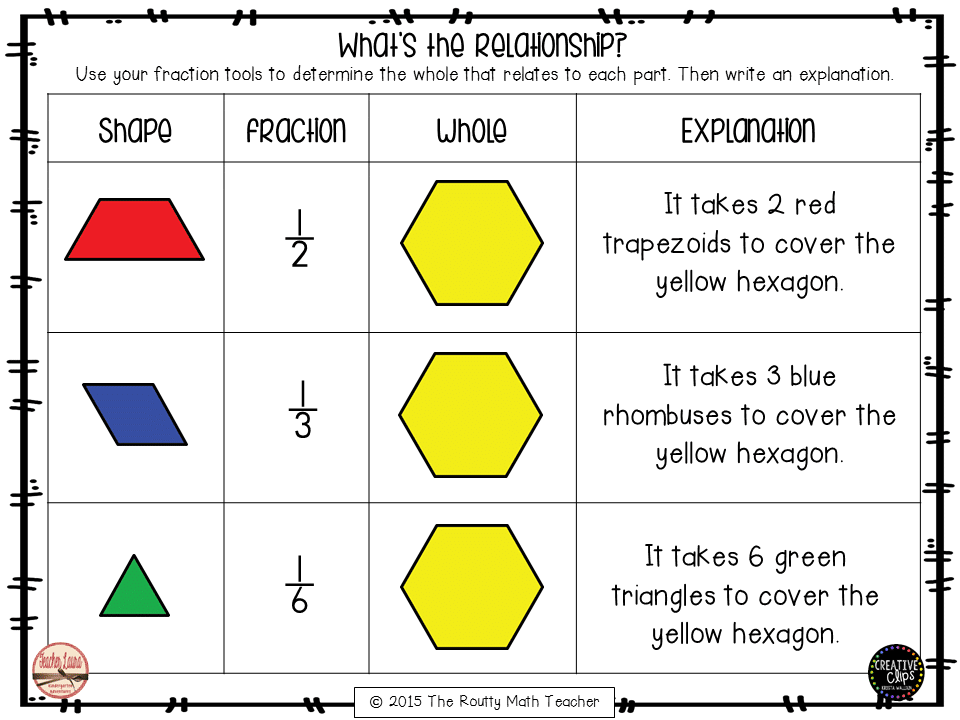
The CCSSM standard above requires students to understand how to relate an individual piece to the whole using the formal fraction notation. The yellow hexagon, red trapezoid, blue rhombus, and green triangle shapes in a pattern block set fit together perfectly to model fractional relationships. Pattern blocks can be used to help students make the connection between the size of the part, named fraction, and the number of parts that make up the whole. The “What’s the Relationship?” chart below illustrates how this can be accomplished.
Fraction Tiles
Common Core State Standards:
- 4.NB.B.3.- Understand a fraction a/b with a > 1 as a sum of fractions 1/b.
- 4.NF.B.3.A.- Understand addition and subtraction of fractions as joining and separating parts referring to the same whole
- 4.NF.B.3.B- Decompose a fraction into a sum of fractions with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g. by using a visual fraction model.
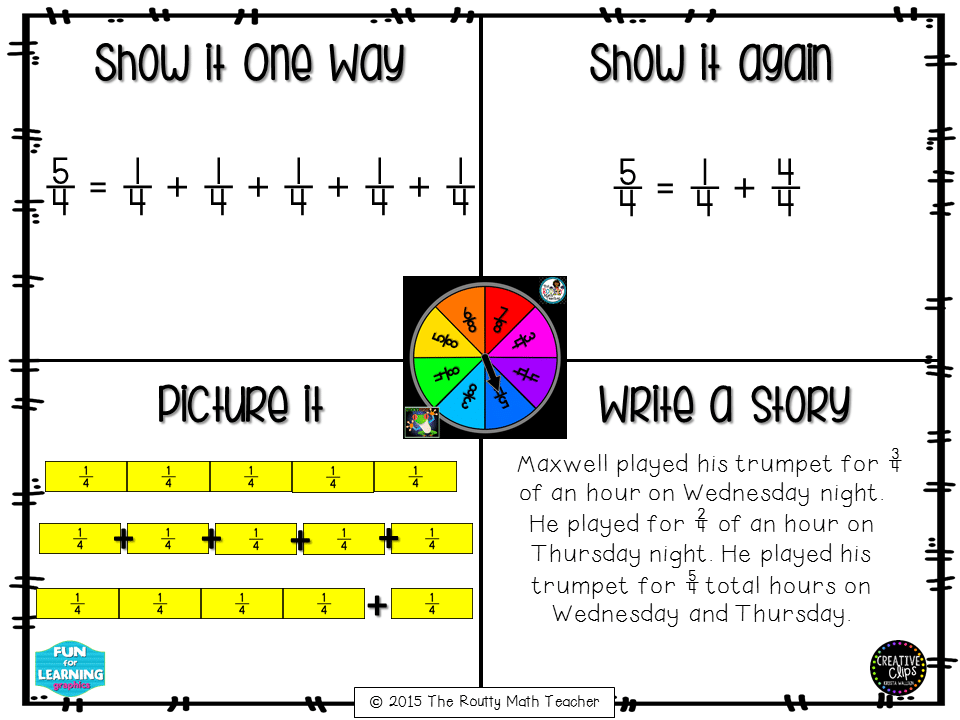
Building a strong foundation for fractions in the early grades provides long-term support for the development of fraction operations in the upper grades. Students begin fraction operations by decomposing fractions into fractions with the same denominator. Understanding how to decompose fractions supports the following essential fraction understandings:
- understand the meaning and purpose of the numerator, denominator, and unit (or whole)
- addition of fractions is an extension of whole number addition and involves joining or combining disconnected parts
- addition sequences can represent different problem situations
- the interpretation of a problem situation can lead to different representations
- the denominators of the addends remain the same and are not added together
- addition and subtraction of fractions refer to the same unit, or whole
- show the decomposition another way
- write a story to match the equation
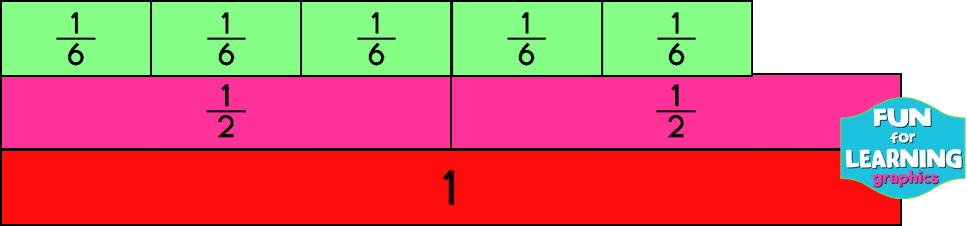
Fraction Bars
Common Core State Standard 5.NF.A.2- Solve word problems involving addition and subtraction of fractions referring to the same whole, including cases of unlike denominators, e.g., by using visual fraction models or equations to represent the problem. Use benchmark fractions and number sense of fractions to estimate mentally and assess the reasonableness of answers.
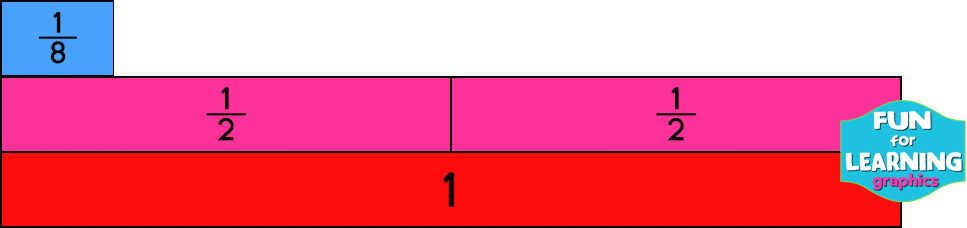
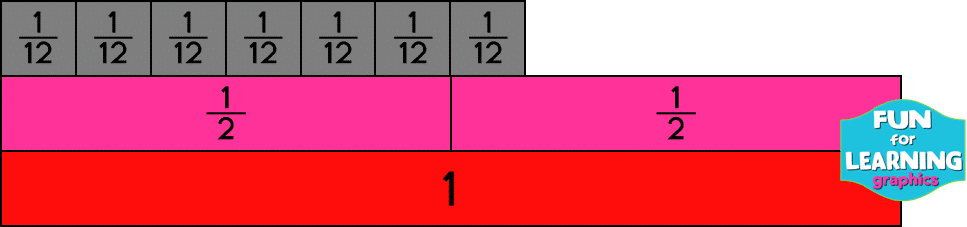
Students struggle to understand how to make sense of the value of a fraction. A few years back, in an effort to try to help my fourth graders really make connections between the value of a fraction and the formal fraction notation, I taught them how to compare the fraction to a benchmark. Each time I presented a fraction, I posed the question, “Is this fraction closer to zero, one-half, or one whole?” And, I often added, “How do you know?” Using benchmark fractions gave the students a reference to use in their comparisons.
It took some time, but I began to notice that my students’ understanding of fractions developed into the deeper understanding I had envisioned. (An understanding that prevents the dreaded one-third plus one-third equals two-sixths because using benchmark fractions will allow students to see that one-half (the benchmark for one-third) plus one-half equals one whole. Therefore, the solution for one-third plus one-third should be closer to one whole. Two-sixths is closer to zero, not one whole.)
It’s important to note that students don’t just develop this understanding without beginning with the conceptual models. Students need lots of opportunities to make the comparisons using fraction tools before being able to make a visual estimation from the formal notation. See the examples using fraction bars below.

Like the resource pages above?
You can find them in the Common Core Aligned Resources section of my file cabinet.
Sound Off! What are your favorite fraction tools? Respond in the comments section below.








3 Responses
Dear Shametria,
I am a preservice math teacher and I believe many students may benefit if their teachers had a deeper understanding of fractions. I see in your post you have addressed the standards and multiple different activities students can participate in to gain a better understanding of fractions. How do you suggest teachers can help make sense of what it means when multiplying fractions? For example, how would you explain to students why you multiply across the top and multiply across the bottom when multiplying fractions?
Thank you,
Vishna Patel
Great question! A deep understanding of fractions begins with a strong conceptual approach. Working with students to understand what it means to multiply with fractions and how to create a model that illustrates the concept is most important. When students begin connecting the model to a written method, they will begin to understand the standard algorithm. For example, think about three groups of two-fifths (3/1 x 2/5). With a model, students will discover that three groups of two-fifth equals six-fifths. When you connect to the written method, students will see that 3 x 2 = 6 and 1 x 5 = 5, so six-fifths. After completing enough examples, especially with a fraction times a fraction, the algorithm develops itself!
Thank you for the resources they are amazing!