Halloween Math Activities

During my first few years in the classroom, my theme was the same every year.

Garfield . . . need I say more. 😁

Now, some of you youngsters may not have any idea what I am talking about, but I LOVED Garfield and Odie. 

Over the years, I collected more Garfield posters than I could count. I even had two-foot-tall Garfield and Odie stuffed animals that I prominently displayed in the classroom. 

I know, I know. 

And, at the beginning of each school year, I taped my favorite Garfield poster to the front of my classroom door. 

“Welcome to class. You may start thinking now.”

It let my students know right from the start what I expected from them . . . to think. 

Revving Up the Engine

At the start of class, I presented students with a math starter, a quick critical thinking activity, to charge up their brains and get them ready for the lesson. 

Designed to take no more than 5 – 10 minutes of instructional time, math starters include a variety of critical thinking tasks. I typically do a different starter each day to give the students’ brains a real workout.

A Little Halloween Math Fun

To celebrate October, I created five Halloween math activities to engage your students and get them thinking critically about math. These activities target students in grades 3 – 5; however, with a little creative adaptation, you can modify them to meet the needs of younger grades.

After introducing each activity, I provide guiding questions and differentiation tips. In addition, an answer key is provided at the end of each section.

Task 1: Estimation 180

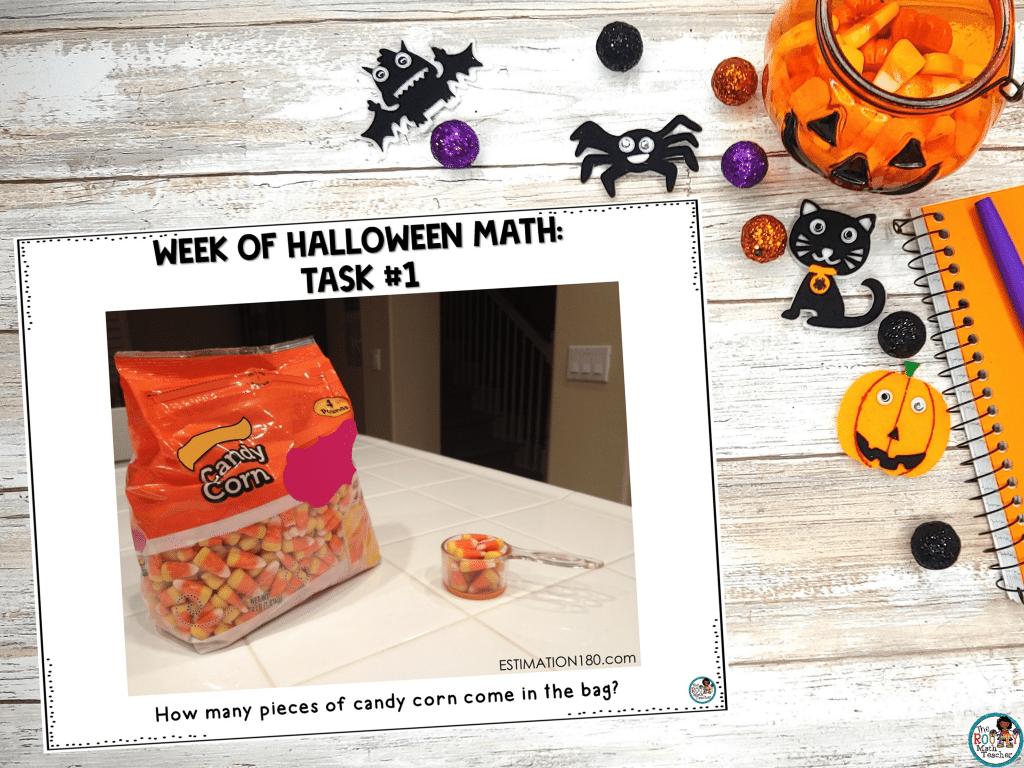
This activity is from a website called Estimation 180 where students use a picture to estimate some quantity related to the elements of the picture.

For this particular task, students are asked to estimate how many candies are in the bag. To do this, students need to first estimate the number of scoops in the bag and then the number of candies in the scoop. Once they obtain these two quantities, they can multiply the number of scoops by the number of candies in one scoop.

The beauty of this task is the discussion piece. Listening to students communicate about how they arrived at their estimates will reveal a lot about their thinking.

The creators of the website also emphasize discussion surrounding estimates that are too low or too high and the thinking required to rule out a certain quantity.

Solution: About 893 candies

Variation: Try a different candy corn problem such as estimating the number of candy corns in the scoop or estimating the number of scoops to fill a jar.

Task 2: Logic Puzzle

The next activity is a logic puzzle. Students use the information they glean from the puzzle to determine the numerical value of each symbol. To help them, the sum of each row and column is shown on the outside of the table.

At first glance, this puzzle may seem challenging for some students. The secret to solving it is to look for the best place to start. Then, probe further to ensure students understand why one starting position may be better than another.

Use the questions below to support students during productive struggle.

a. Where is a good place to start? How do you know?

b. Once you believe you have determined the value of one of the symbols, how can you use the information to keep you moving forward?

c. How can you use the sums on the perimeter to check your work?

d. How will you know when you have completed the puzzle correctly?

Solution: Witch = 12, Pumpkin = 8, Black Cat = 4, Vampire = 2

Variation: Change the sums to smaller or larger numbers. For example, divide each sum by two to provide support for younger students or those who need a simpler task. Consider using decimal values to represent the symbols for older students.

Task 3: Traditional Problem Solving

This task is a traditional problem-solving scenario. To get the most from this task, allow students an opportunity to complete the problem individually or with a partner before discussing the task together. Students then record their thinking and their solution strategy on paper.

While students work through the task, use the questions below to support student thinking.

a. What do you know about the boys’ ages?

b. What information can you use to help you get started?

c. What process will you use to solve the problem?

d. How will you know when you have found the right solution?

After students have an opportunity to complete the task, review the students’ solution strategies as a class and discuss the most effective and efficient methods for completing the task. 

Solution: Gomez is 7 years old, Pugsley is 12 years old, and Frankenstein is 15 years old.

Variation: For younger students or for students who need a simpler task, change the task to say- “Young Frankenstein has two brothers, Pugsley and Gomez. The sum of their ages is 34. Frankenstein is older than Pugsley, but Pugsley is not the youngest. Gomez is 8 years younger than Frankenstein who is 16 years old. How old are the three brothers?”

Task 4: Number Logic Tiling Task

Of all the tasks, tiling tasks are my favorite! This set requires students to analyze number sentences and determine a number from a set of 0–9 labeled tiles to represent each symbol. Each tile represents one and only one symbol.

This task also emphasizes all four operations, logic, and algebraic thinking. Initially, the task may look intimidating; however, like the logic task above, the secret is to find the best place to start. 

After students complete the task, discuss the ways students approached the task with questions such as:

a. How did you determine where to start?

b. Which number sentences helped you “narrow down” the possible solutions?

c. What did you do when you were stuck?

d. For which number sentence was it easiest to determine the value of the symbol?

e. In what order did you complete the task?

f. How do you know your solution is correct?

Solution: Cat = 4, Pumpkin = 0, Swirl Candy = 2, Candy Bar = 3, Candy Corn = 6, Bat = 7, Polka-Dot Candy = 8, Ghost = 5, Witch’s Hat = 9, Spider = 1

Variations: Allow students to work in groups or complete the task together as a class.

Task 5: Which One Doesn’t Belong?

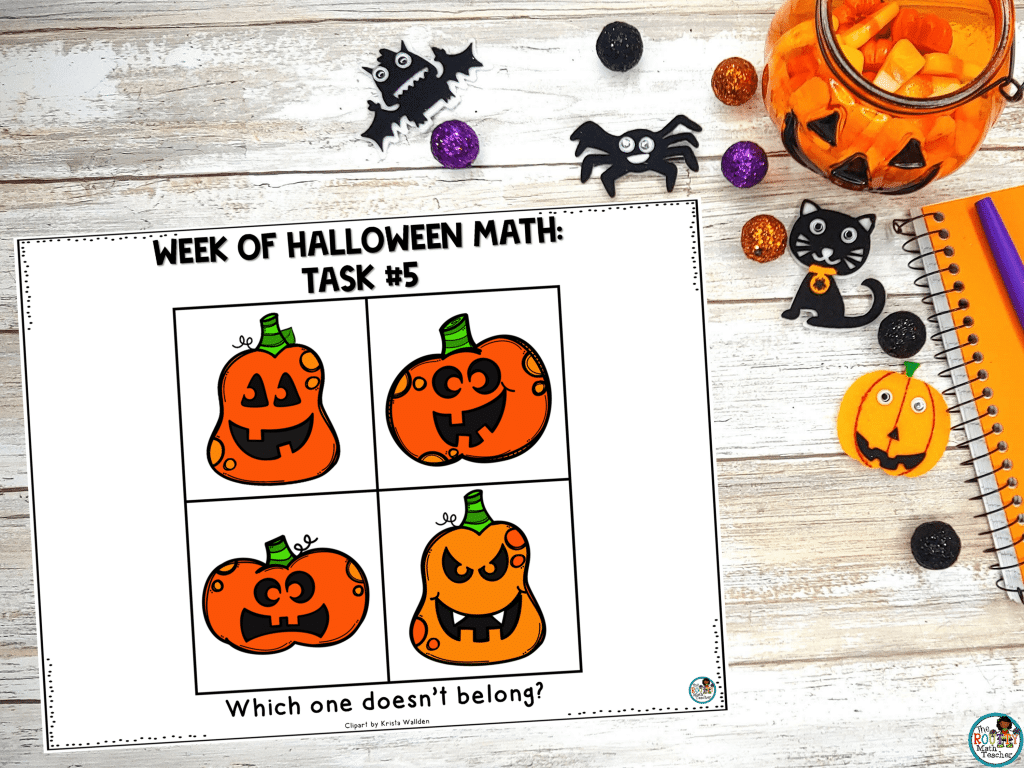
The last task is open-ended. In fact, as long as students can justify their response as to why one pumpkin is out but the others are in, their answer is correct.

This is a great opportunity to allow students to get creative with their reasoning. Here are a few examples of characteristics to use to exclude a pumpkin: pumpkin color, the shape of the eyes, the shape of the mouth, number of teeth, curly “q” off of the stem, etc.

For this task, you may want to divide your room into four sections and assign each section a pumpkin. Then have students go to the section for the pumpkin they feel does not belong.

Once divided into groups, have each group discuss what defining characteristic they used to exclude the pumpkin. As students discuss, be sure to wander around and listen to the variety of ways students excluded the same pumpkin. Then, have each group share some of their reasoning.

Solution: Answers will vary depending on the elimination criteria used. Remember, the best of this task is to look at all the possibilities.

Variation: Because this is such an open-ended task, it is accessible to a wide variety of students and will naturally vary by the characteristics students select as their elimination criteria.

Let’s Celebrate The Season!

It’s not just Shocktober for teachers, it feels that way for our students too. Let’s take this opportunity to celebrate the season with these fun Halloween math activities.

Grab your set using the form below. They can be shared virtually, displayed on a projector, or placed under a document camera.

Sound Off!

Which Halloween math activities are you most excited about trying with your students? Why? Respond in the comments below.